Integración numérica

4.4. Integración numérica#

4.4.1. Casos en los que se utiliza#

Hay algunos casos en los que, en vez de buscar la primitiva de una función y aplicar la regla de Barrow, usaremos una fórmula de integración numérica. Sobre todo cuando

  • Sólo conocemos los valores de la función en un número finito de puntos.

  • Su primitiva no se expresa en términos de funciones elementales. Por ejemplo:

\[ \int \frac{\sin x}{x} \,dx;\qquad \int e^{-x^2}\,dx. \]

  • Su primitiva es muy costosa de calcular o evaluar. Por ejemplo:

\[ \int \frac{1}{(x-8)\sqrt{x^2-4x-7}} \, dx. \]

Definition (Fórmula de integración numérica o de cuadratura)

Una fórmula de integración numérica o fórmula de cuadratura es una suma de la forma:

\[ \sum_{i=0}^n\omega_i\,f(x_i)\approx \int_a^bf(x)\,dx, \]

donde los puntos \(x_0\), \(x_1\), …, \(x_n\) son los llamados nodos de cuadratura y los valores \(\omega_0\), \(\omega_1\), …, \(\omega_n\) son los pesos asociados a cada nodo.

4.4.2. Fórmulas simples#

  • Fórmula del punto medio:

    \[ \int_a^bf(x)\,dx\,\simeq\,(b-a)\,f\left(\frac{a+b}{2}\right) \,. \]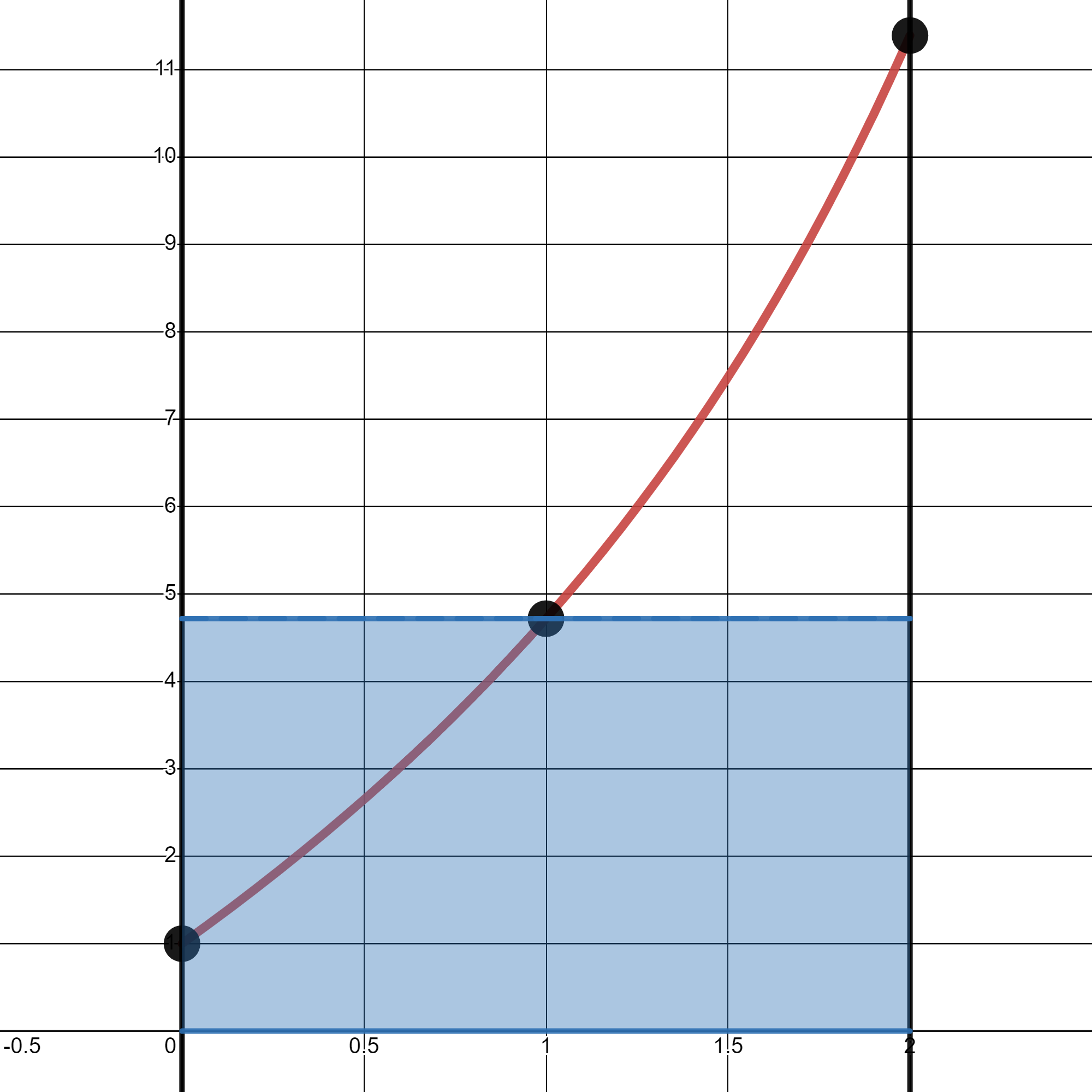
    ../../_images/cap4_punto_medio.png

  • Fórmula del trapecio:

    \[ \int_a^bf(x)\,dx\,\simeq\,\frac{b-a}{2}\,\big(f(a) + f(b)\big) \]
    ../../_images/cap4_trapecio.png

  • Fórmula de Simpson: Está basada en una interpolación cuadrática (tres nodos):

    \[ \int_a^bf(x)\,dx \,\simeq\, \frac{b-a}{6}\,\Big(\,f(a)\,+\,4\,\, f(\frac{a+b}{2})\,+\,f(b)\Big) \]
    ../../_images/cap4_simpson.png

Example

Determinar una aproximación de \(\displaystyle \int_1^3 \sin(\sqrt{x}) \, dx\) mediante las fórmulas del trapecio y de Simpson, y comparar con la solución exacta:

Tomando el cambio de variable \(u = x^{1/2}\) e integrando por partes llegamos a:

\[ \displaystyle \int \sin(\sqrt{x}) \, dx = 2 \sin(\sqrt{x}) - 2 \sqrt{x} \cos(\sqrt{x}) + C; \quad \displaystyle \int_1^3 \sin(\sqrt{x}) \, dx = 1.9279... \]

Mientras que por integración numérica:

\[\begin{eqnarray*} &\bullet& \quad \text{Trapecio: }\displaystyle \int_1^3 \sin(\sqrt{x}) \simeq \frac{3 - 1}{2}\big(\sin(1) + \sin(\sqrt{3}) \big) = 1.8285...\\ &\bullet& \quad \text{Simpson: } \displaystyle \int_1^3 \sin(\sqrt{x}) \simeq \frac{3 - 1}{6}\big(\sin(1) + 4 \sin(\sqrt{2}) + \sin(\sqrt{3}) \big) = 1.9265... \end{eqnarray*}\]

La fórmula de Simpson tiene en cuenta un nodo más que la del trapecio y en este ejemplo podemos ver que arroja una mejor aproximación.

4.4.3. Fórmulas compuestas#

La idea es sencilla: se divide el intervalo de integración, \([a,b]\), en subintervalos y en cada uno de estos se usa una fórmula de integración numérica simple.

El caso más habitual surge cuando tomamos \(n\) subintervalos, \([x_i, x_{i + 1}]\), de igual longitud \(h\). Es decir, cuando elegimos \(x_i = a + ih\), \(i = 0, 1, ..., n\), para un valor \(h = \frac{b - a}{n}\).

Entonces aproximamos la integral mediante una fórmula simple en cada subintervalo. Pero, ¡cuidado!:

  • para punto medio o Simpson los intervalos los tenemos que tomar los intervalos de tamaño \(2h\), es decir, de 3 en 3 puntos, porque necesitamos el punto medio de cada subintervalo, \([x_{2i-2}, x_{2i}]\),

  • para trapecio, como no necesitamos el punto medio, podemos tomar todos los subintervalos que, en este caso, tendrán tamaño \(h\): \([x_{i}, x_{i-1}]\).

Entonces tendremos:

  • Punto medio o Simpson compuestos, con \(n\) par: \(\displaystyle \int_a^b f(x)\,dx = \sum_{i=1}^{n/2} \int_{x_{2i-2}}^{x_{2i}} f(x)\,dx\).

  • Trapecio compuesto: \(\displaystyle \int_a^b f(x)\,dx = \sum_{i=0}^{n} \int_{x_{i-1}}^{x_{i}} f(x)\,dx\).

Ahora, dependiendo de la fórmula simple que elijamos tendremos:

  • Fórmula del punto medio compuesta:

    \[\begin{eqnarray*} \int_a^b f(x)\,dx = \sum_{i=1}^{n/2} \int_{x_{2i-2}}^{x_{2i}} f(x)\, dx &\approx& \sum_{i=1}^{n/2} \left(x_{2i}-x_{2i-2}\right) f\left(x_{2i-1}\right) \\ &=& 2h\sum_{i=1}^{n/2} f\left(x_{2i-1}\right) \end{eqnarray*}\]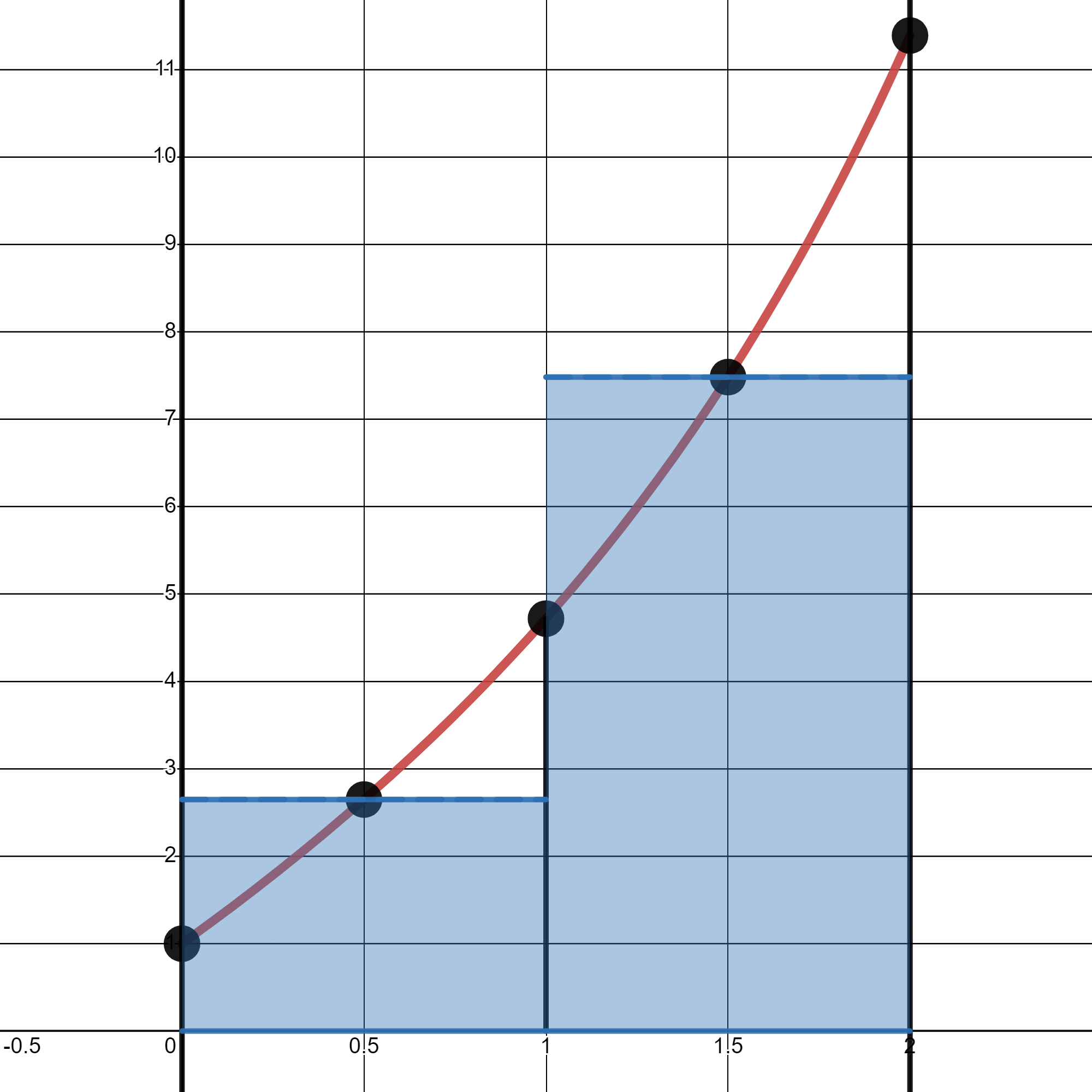
    ../../_images/cap4_punto_medio_compuesto.png

  • Fórmula del trapecio compuesta:

    \[\begin{eqnarray*} \int_a^b f(x)\,dx = \sum_{i=1}^{n} \int_{x_{i-1}}^{x_{i}} f(x)\, dx &\approx& \sum_{i=1}^{n} \frac{h}{2} \left( f\left(x_{i-1}\right) + f\left(x_{i}\right) \right) \\ &=& \frac{h}{2} \left( f(x_{0}) + 2 \sum_{i=1}^{n-1}f(x_{i}) + f(x_{n}) \right) \end{eqnarray*}\]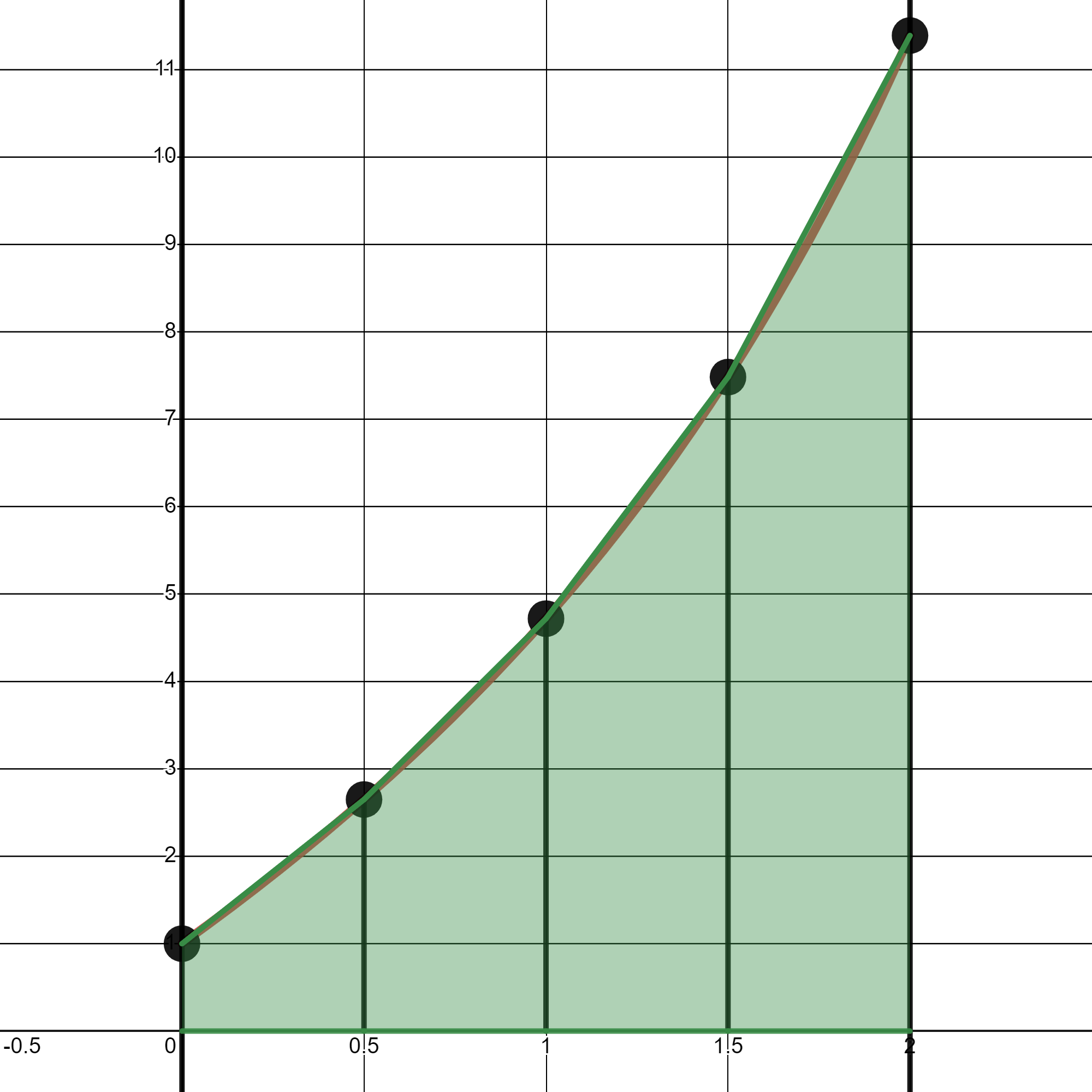
    ../../_images/cap4_trapecio_compuesto.png

  • Fórmula de Simpson compuesta:

    \[\begin{eqnarray*} \int_a^b f(x)\,dx = \sum_{i=1}^{n/2} \int_{x_{2i-2}}^{x_{2i}} f(x)\, dx &\approx& \sum_{i=1}^{n/2} \frac{2h}{6} \left(f\left(x_{2i-2}\right) + 4f\left(x_{2i-1}\right) + f\left(x_{2i}\right) \right) \\ &=& \frac{2h}{6} \left( f(x_{0}) + 4\sum_{i=1}^{n/2} f(x_{2i-1}) + 2\sum_{i=1}^{n/2-1}f(x_{2i}) + f(x_{n}) \right) \end{eqnarray*}\]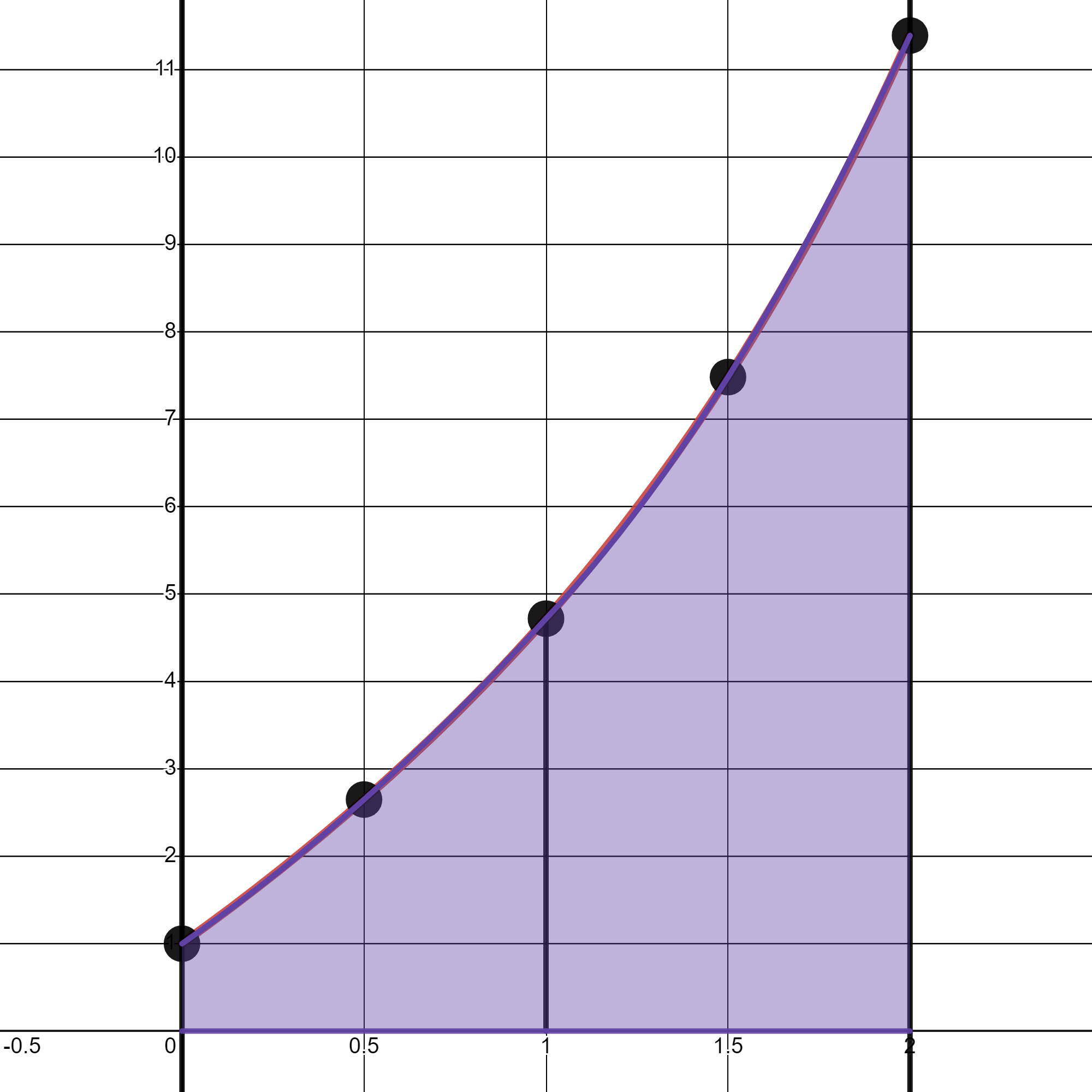
    ../../_images/cap4_simpson_compuesto.png

4.4.4. Integración numérica con Numpy#

4.4.4.1. Fórmulas simples#

A continuación mostramos las functions que nos permiten la programación de las fórmulas simples que acabamos de ver en Numpy y un ejemplo de su aplicación.

Probaremos sobre

\[ I=\int_{0}^{3}\left(x^4+1\right)\,dx\,, \]

ya que, en este caso sencillo, podemos conocer el valor exacto de la integral:

\[ I=\int_{0}^{3}\left(x^4+1\right)\,dx = \left[\frac{x^5}{5}+x\right]_{x=0}^{3} = \frac{3^5}{5}+3 = 51.6\, . \]
import sympy as sp
import numpy as np

def pto_medio(a, b, fpm):
    aprox_pm = (b-a) * fpm
    return aprox_pm

def trapecio(a, b, fa, fb):
    aprox_tr = (b-a) * (fa + fb)/2
    return aprox_tr

def simpson(a, b, fa, fpm, fb):
    aprox_simp = (b-a) * (fa + 4*fpm + fb)/6
    return aprox_simp

x = sp.Symbol('x', real = True)

f_exp = x**4 + 1
f = sp.lambdify(x,f_exp)

a = 0
b = 3
pm = (a+b)/2

fa = f(a)
fpm = f(pm)
fb = f(b)

print('Valor aproximado de I mediante la fórmula del punto medio = ', pto_medio(a,b,fpm) ) 
print('Valor aproximado de I mediante la fórmula del trapecio = ', trapecio(a,b,fa,fb) ) 
print('Valor aproximado de I mediante la fórmula de Simpson = ', simpson(a,b,fa,fpm,fb) ) 

Valor aproximado de I mediante la fórmula del punto medio =  18.1875
Valor aproximado de I mediante la fórmula del trapecio =  124.5
Valor aproximado de I mediante la fórmula de Simpson =  53.625

4.4.4.2. Fórmulas compuestas#

Como puedes ver en el apartado anterior, las fórmulas simples pueden dar resultdos bastante… pésimos.

Vamos a implementar ahora de manera eficiente las fórmulas compuestas utilizando la función de np.sum.

import sympy as sp
import numpy as np

x = sp.Symbol('x', real = True)
f_exp = x**4+1
f = sp.lambdify(x,f_exp)

a = 0; b = 3
n = 100

x1 = np.linspace(a,b,n+1) # aquí guardamos los x_{i}. 
                          # Recuerda que, en Python, se guarda x1[0], x1[1], ..., x1[(n+1)-1] = x1[n]
y1 = f(x1)

h = (b-a)/n # el tamaño de cada subintervalo

aprox_trap = h/2 * (y1[0]+2*np.sum(y1[1:n])+y1[n])
aprox_medio = 2*h * np.sum(y1[1:n:2])
aprox_simpson = 2*h/6 * (y1[0] + 4*np.sum(y1[1:n:2])+2*np.sum(y1[2:n-1:2])+y1[n])

print('aprox_trap: ',aprox_trap) 
print('aprox_medio: ',aprox_medio) 
print('aprox_simpson: ',aprox_simpson) 

print('Exacta: ',b**5/5+b)

aprox_trap:  51.608099919
aprox_medio:  51.583801133999984
aprox_simpson:  51.60000032399999
Exacta:  51.6

4.4.5. Más información#

Y ahora os damos alguna referencia para que, si os apetece, ampliéis vuestro conocimiento sobre integración numérica:

Contents