5.5. Derivación en Python

Esta sección pretende ser un compendio (esperemos que claro y ordenado) de todo el Python que hemos ido usando en el Capítulo 3.

Objetivos:

• Cálculo de derivadas con Sympy.

• Implementación en Numpy del método numérico de Newton-Raphson.

• Derivadas sucesivas con Sympy.

• Uso de Python en problemas de máximos y mínimos.

• Cálculo, con Sympy, del polinomio de Taylor y del resto.

5.5.1. Derivación en Sympy

La realizaremos con el comando sp.diff, como mostramos en el siguiente ejemplo:

import sympy as sp
x=sp.symbols('x')
f_exp=sp.exp(x)*sp.cos(x)
d1f_exp=sp.diff(f_exp,x)
print('Para la función: ',f_exp)
print('La derivada primera es: ',d1f_exp)

Para la función:  exp(x)*cos(x)
La derivada primera es:  -exp(x)*sin(x) + exp(x)*cos(x)

5.5.2. Implementación en Numpy del método numérico de Newton-Raphson

Mostramos a continuación una implementación directa, mediante un bucle, de este método:

import numpy as np
import sympy as sp

x = sp.symbols('x', real=True) # define la variable simbólica x

f_expr = x**3+2*x-2
f_der_expr = sp.diff(f_expr,x)

f = sp.Lambda(x,f_expr)
f_der = sp.Lambda(x,f_der_expr)

N_max = 10
tol = 1.e-9

x_aprox = np.zeros(N_max)
x_aprox[0] = 2

for k in range(1,N_max):
    if ( np.abs( f_der(x_aprox[k-1]) ) < 1.e-14 ): break

    x_aprox[k] = x_aprox[k-1] - f(x_aprox[k-1])/f_der(x_aprox[k-1])

    if ( (k > 0) and (np.abs(x_aprox[k]-x_aprox[k-1]) / np.abs(x_aprox[k]) < tol) ): break

print('Número de iteraciones realizadas: ', k) 
print('Aproximación de la raíz: ', x_aprox[k])

Número de iteraciones realizadas:  7
Aproximación de la raíz:  0.7709169970592481

En la Sección Método de Newton-Raphson puedes ver el gráfico de este caso con Matplotlib.

5.5.3. Derivadas sucesivas con Sympy

Para calcular derivadas sucesivas en Sympy tenemos que añadir un parámetro en sp.diff que indique el número de veces que queremos derivar:

import sympy as sp

x = sp.symbols('x', real=True)
f_exp = sp.sin(x) + x**2
print('Expresión que queremos derivar: ',f_exp)
print('Primera derivada: ',sp.diff(f_exp,x))
print('Segunda derivada: ',sp.diff(f_exp,x,2))
print('Tercera derivada: ',sp.diff(f_exp,x,3))
# Nota: también se puede usar la siguiente escritura:
# print(f_exp.diff(x,3))

Expresión que queremos derivar:  x**2 + sin(x)
Primera derivada:  2*x + cos(x)
Segunda derivada:  2 - sin(x)
Tercera derivada:  -cos(x)

5.5.4. Uso de Python en problemas de máximos y mínimos

Dado un canal de sección trapezoidal de lado 2, calcular el ángulo \(\alpha\) (ver dibujo) que maximiza el área de la sección del canal.

1. A mano. Obtener la función que proporciona el área del canal en función del ángulo \( \alpha \)

2. Simbólicamente: con Sympy.

3. Numéricamente mediante el método de Newton con error menor que \( 10^{-4} \).

import sympy as sp
# 2. Resolvemos el problema utilizando Sympy
x,xn=sp.symbols('x,xn')
# Funcion que describe el area de la seccion en funcion del angulo
f=4*sp.sin(x)*(1+sp.cos(x))
d1f=sp.diff(f,x)
d1fn=sp.lambdify(x,d1f)
alphamax=sp.solve(d1f)
print('La sección máxima se alcanza con ángulo: ',float(alphamax[1]))

La sección máxima se alcanza con ángulo:  1.0471975511965979

# 3. Aproximamos el máximo con el método de Newton
maxit=100
eps=1e-4
d2f=sp.diff(d1f,x)
d2fn=sp.lambdify(x,d2f)
xn=np.pi/2
for i in range(0,maxit):
    res=d1fn(xn)/d2fn(xn)
    xn=xn-res
    if (np.abs(res)<eps):
        break
print('Numero de iteraciones realizadas: ',i)
print('Aproximación del ángulo para la sección máxima con NR: ',xn)

Numero de iteraciones realizadas:  4
Aproximación del ángulo para la sección máxima con NR:  1.0471975511965559

5.5.5. Cálculo, con Sympy, del polinomio de Taylor y del resto.

La siguiente función calcula, de forma simbólica, el polinomio de Taylor de una función dada.

• Argumentos de entrada:

  • expresión f,

  • punto x0, que será el centro de Taylor,

  • orden del polinomio, n.

• Salida:

  • expresión del polinomio de Taylor, p,

  • epresión del resto de Taylor, r.

import sympy as sp

x,t=sp.symbols('x,t')

# p: polinomio de Taylor
# R: resto en valor absoluto
def taylor(f,x0,n):
    p=0
    for i in range(n+1):
        p+=sp.diff(f,x,i).subs(x,x0)/sp.factorial(i)*(x-x0)**i
    R=sp.diff(f,x,n+1).subs(x,t)/sp.factorial(n+1)*(x-x0)**(n+1)
    return p,R

5.5.6. Ejemplo completo de Taylor con Python

Queremos aproximar \(\ln(1.3)\), utilizando polinomios de Taylor de orden \(n=1\) y \(n=2\), centrados en \(x_{0}=1\), para la función \(f(x) = \ln(x)\).

import sympy as sp
import numpy as np

x, t = sp.symbols('x, t', real =True)

# Importamos la function que calcula el polinomio y el resto de Taylor
def taylor(f_exp,x0,n):
    p_exp = 0
    for i in range(n+1):
        p_exp += sp.diff(f_exp,x,i).subs(x,x0)/sp.factorial(i)*(x-x0)**i
        
    R_exp = sp.diff(f_exp,x,n+1).subs(x,t)/sp.factorial(n+1)*(x-x0)**(n+1)
    return p_exp,R_exp

x0 = 1  # punto en el que centramos el polinomio de Taylor

# función que queremos aproximar
f_exp = sp.log(x)

# calculamos el Polinomio de Taylor de orden 1 centrado en x0
n = 1 

P1_exp, R1_exp = taylor(f_exp,x0,n)
print('Polinomio de Taylor de orden 1: \n',P1_exp,'\n Resto de Taylor de orden 1: \n',R1_exp,'\n')

# Creamos una función sp.lambdify del polinomio 
P1 = sp.lambdify (x,P1_exp)
print('Aproximación de ln(1.3) con el polinomio de Taylor de orden 1: ', P1(1.3))

# calculamos el Polinomio de Taylor de orden 2 centrado en x0
n = 2 

P2_exp, R2_exp = taylor(f_exp,x0,n)
print('Polinomio de Taylor de orden 2: \n',P2_exp,'\n Resto de Taylor de orden 1: \n',R2_exp,'\n')

# Creamos una función sp.lambdify del polinomio 
P2 = sp.lambdify (x,P2_exp)
print('Aproximación de ln(1.3) con el polinomio de Taylor de orden 2: ', P2(1.3))

Polinomio de Taylor de orden 1: 
 x - 1 
 Resto de Taylor de orden 1: 
 -(x - 1)**2/(2*t**2) 

Aproximación de ln(1.3) con el polinomio de Taylor de orden 1:  0.30000000000000004
Polinomio de Taylor de orden 2: 
 x - (x - 1)**2/2 - 1 
 Resto de Taylor de orden 1: 
 (x - 1)**3/(3*t**3) 

Aproximación de ln(1.3) con el polinomio de Taylor de orden 2:  0.2550000000000001

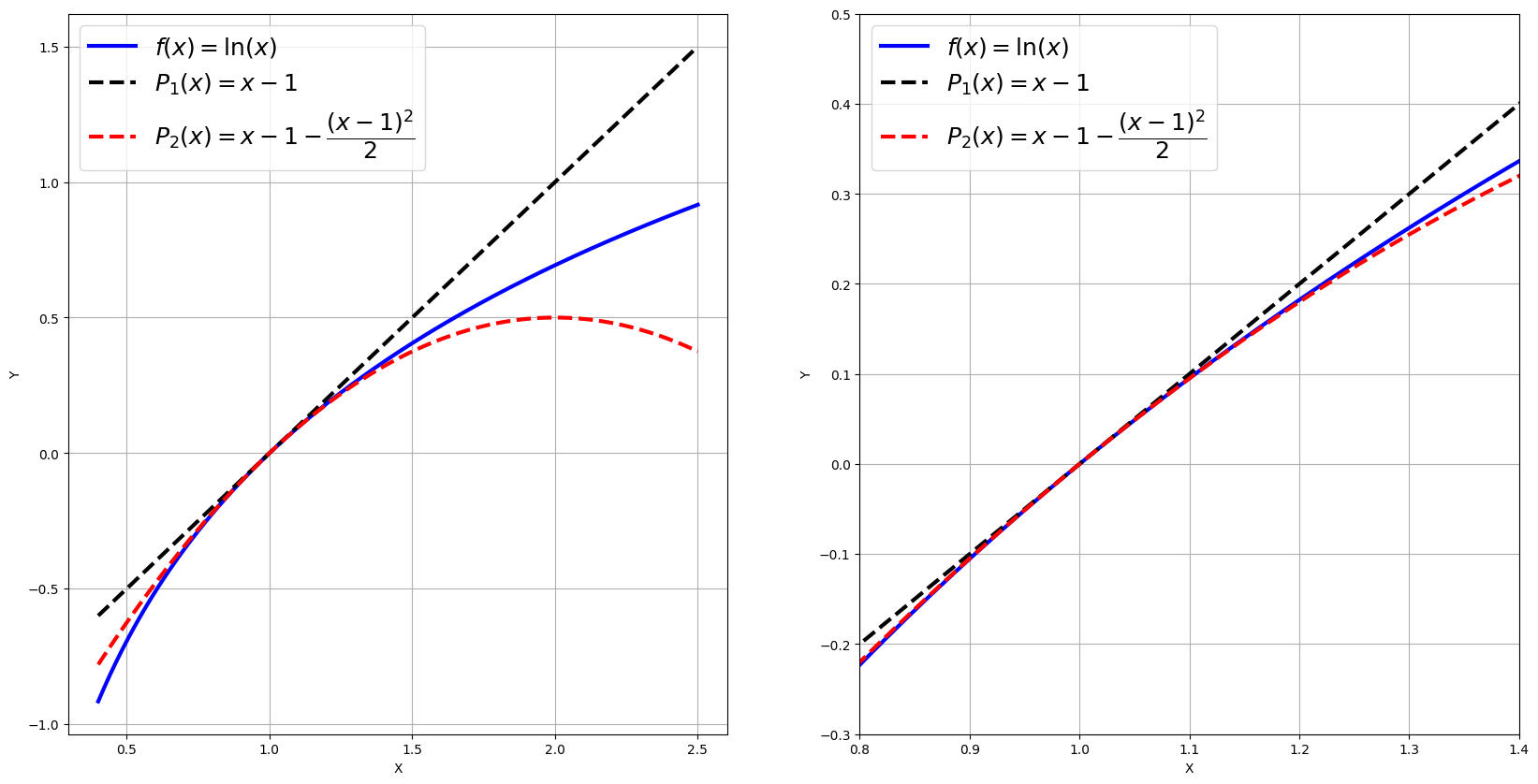
Dibujamos el resultado con Matplotlib:

import matplotlib as mp
import matplotlib.pyplot as plt

# Creamos gráficos de funciones
x1 = np.linspace(0.4, 2.5, 200)
y1 = np.log(x1)

# evaluamos P2 en los puntos de x1
P1x = P1(x1)
P2x = P2(x1)

fig, axs = plt.subplots(1, 2, figsize=(20,10))

ax1 = axs[0]
ax1.plot(x1, y1, c='b', lw='3',  label='$f(x)=\ln(x)$')
ax1.plot(x1, P1x, c='k', ls='--', lw='3', label='$P_1(x)=x-1$')
ax1.plot(x1, P2x, c='r', ls='--', lw='3', label='$P_2(x)=x-1 - \dfrac{(x-1)^2}{2}$')
ax1.set_ylabel('Y', fontsize=10)
ax1.set_xlabel('X', fontsize=10)
ax1.grid()
ax1.legend(prop={'size': 18})


ax2 = axs[1]
ax2.plot(x1, y1, c='b', lw='3', label='$f(x)=\ln(x)$')
ax2.plot(x1, P1x, c='k', ls='--', lw='3', label='$P_1(x)=x-1$')
ax2.plot(x1, P2x, c='r', ls='--', lw='3', label='$P_2(x)=x-1 - \dfrac{(x-1)^2}{2}$')
ax2.set_ylabel('Y', fontsize=10)
ax2.set_xlabel('X', fontsize=10)
plt.xlim(0.8,1.4)
plt.ylim(-0.3,0.5)
ax2.set_xticks(np.arange(0.8,1.5,0.1))
ax2.set_yticks(np.arange(-0.3,0.6,0.1))
ax2.grid()
ax2.legend(prop={'size': 18})

<matplotlib.legend.Legend at 0x242d9ea3c50>

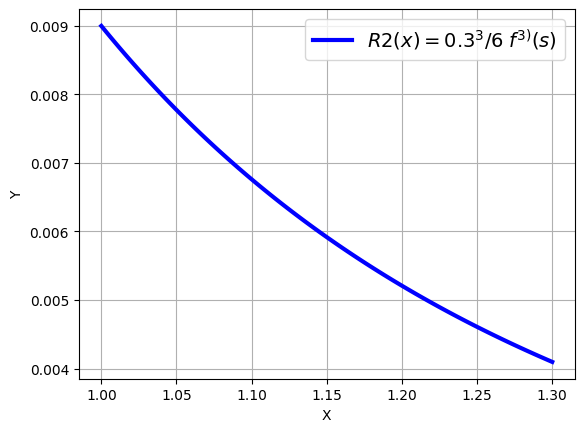
Finalmente, acotaremos el error calculando el máximo del valor absoluto del resto de Taylor de orden 2.

Para ello, en la expresión R2_exp, que hemos obtenido aplicando la function Taylor, sustituimos x por su valor (\(1.3\)). Definimos entonces una función Lamda que dependerá sólo de t y buscamos el máximo, en valor absoluto, de esta función comparando su valor en los extremos y en los puntos en los que se anule su derivada.

R2_exp_xfijo = R2_exp.subs({x:1.3})
R2 = sp.Lambda (t, R2_exp_xfijo)

# Comprobamos que R2 no tiene puntos críticos
ptos_criticos_R2 = sp.solve (sp.diff(R2,x))
print('ptos_criticos_R2: ',ptos_criticos_R2)

# Elegimos el máximo de R2, en valor absoluto, comparando sus valores en los extremos del intervalo
cota_error = sp.Max( sp.Abs(R2(1.)), sp.Abs(R2(1.3)) )

print('Cota del error: ',cota_error)

# Dibujamos R2 en [1,1.3]
R2_vec = sp.lambdify(t,R2_exp_xfijo)
s1 = np.linspace(1, 1.3, 100)
R2_s1 = R2_vec(s1)
plt.plot(s1, R2_s1, c='b', lw='3',  label='$R2(x)=0.3^{3}/{6}\; f^{3)}(s)$')
plt.ylabel('Y', fontsize=10)
plt.xlabel('X', fontsize=10)
plt.grid()
plt.legend(prop={'size': 14})
plt.show()

ptos_criticos_R2:  []
Cota del error:  0.00900000000000000