Aplicaciones de la integral

4.6. Aplicaciones de la integral#

En esta sección vamos a estudiar dos aplicaciones inmediatas de la integral de Riemann: el cálculo de áreas de superficies planas y el volumen de sólidos de revolución.

4.6.1. Cálculo de áreas#

4.6.1.1. Cálculo del área bajo la gráfica de una función positiva#

Dada una función integrable \(f:[a,b]\to R\), \(f(x)\geq 0\) para todo \(x\in [a,b]\) el área de la superficie limitada por la gráfica de \(f\), el eje \(OX\) y las rectas \(x=a,x=b\) viene dada por

\[ A=\int_a^b f(x) dx \]

Ejemplo:

Vamos a detallar un ejemplo que incluye alguna integral un poco más difícil que las que vienen siendo habituales. Queremos deducir una fórmula que todas y todos conocemos bien: el área de un círculo de radio r.

Empezamos fijándonos en que un semicírculo de radio \(r\) está limitado superiormente por la función \(f(x)=\sqrt{r^2 - x^2}\), como mostramos en la siguiente figura.

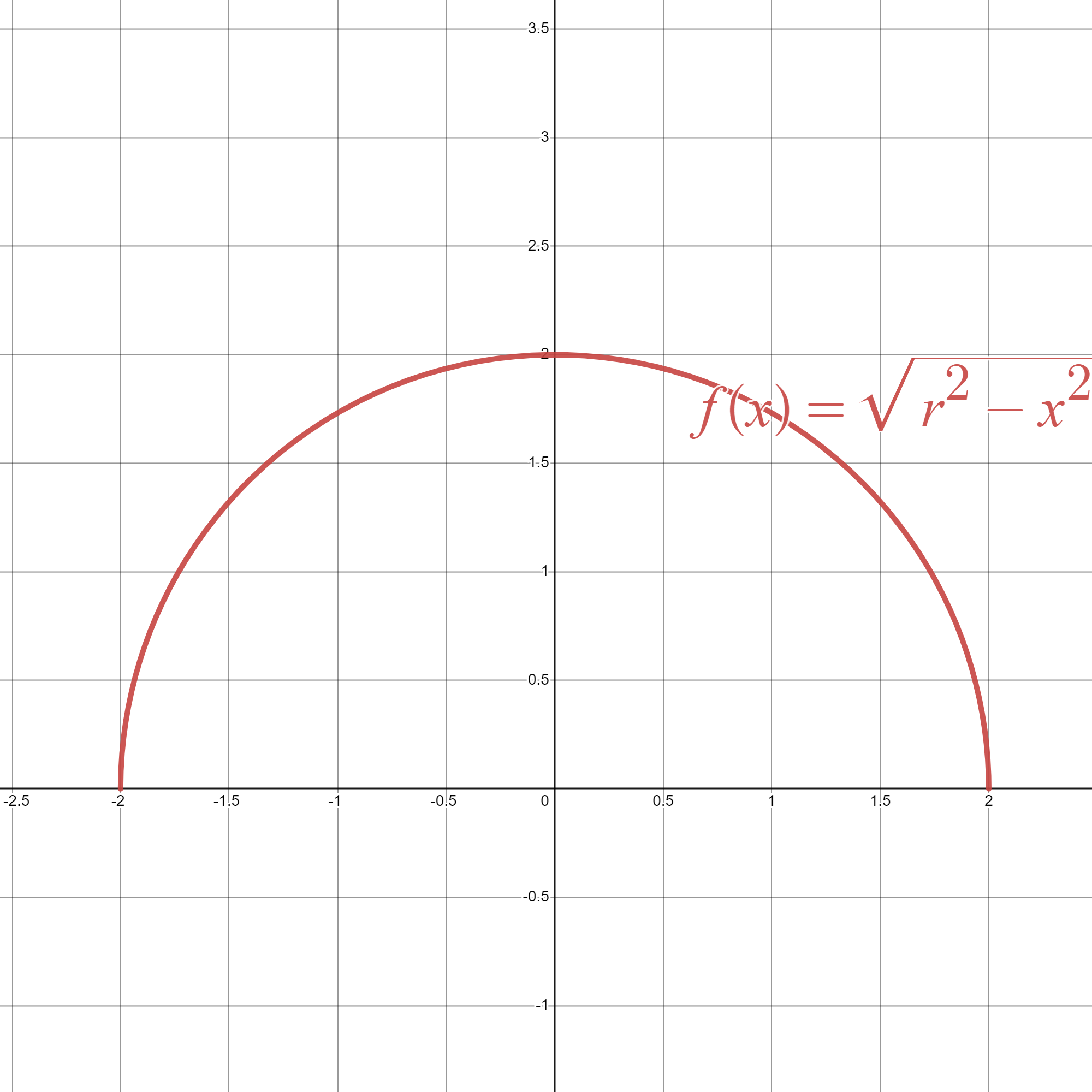
../../_images/cap4_aplicaciones_1.png

Entonces:

\[ A=2\int_{-r}^{r} \sqrt{r^2-x^2} dx \stackrel{(*)}{=} \]

Para resolver esta integral aplicamos el cambio trigonométrico \(x=r\sin(t)\). Fijémonos que \(r\) es un dato del problema, por lo que la nueva variable será \(t\). Entonces \(dx = r\cos(t) \, dt\). También tenemos que cambiar los límites de integración:

  • Límite inferior: \(x=-r \Rightarrow t=\arcsin\left(\frac{-r}{r}\right) = \arcsin(-1) = -\frac{\pi}{2}\).

  • Límite superior: \(x=r \Rightarrow t=\arcsin\left(\frac{r}{r}\right) = \arcsin(1) = \frac{\pi}{2}\).

Entonces, la integral del principio se transforma en

\[ \stackrel{(*)}{=} 2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{r^2-r^2\sin^2(t)}\, r\cos(t)\, dt = 2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{1-\sin^2(t)}\, r^2\cos(t)\, dt = 2r^2\int_{-\pi/2}^{\pi/2} \cos^2 (t) dt \stackrel{(**)}{=} \]

Y ahora tenemos que usar la relación trigonométrica \(\cos^2(t)=\dfrac{1+\cos(2t)}{2}\) para obtener una integral inmediata:

\[ \stackrel{(**)}{=} 2r^2\int_{-\pi/2}^{\pi/2} \frac{1+\cos(2t)}{2} dt = 2r^2\left( \frac{t}{2} + \frac{\sin(2t)}{4} \right] _{-\pi/2}^{\pi/2} = \pi r^2. \]

Por supuesto, este trabajo se lo podemos dejar a Sympy:

import sympy as sp
x = sp.Symbol('x', real=True)
r = sp.Symbol('r', positive=True)
t = sp.Symbol('t')
f_exp = sp.sqrt(r**2-x**2)
A = 2*sp.simplify(sp.integrate(f_exp,(x,-r,r)))
print('El area del circulo de radio r es: ')
display(A)

El area del circulo de radio r es:
\[\displaystyle \pi r^{2}\]

4.6.1.2. Cálculo del área comprendida entre la gráfica de dos funciones#

Dadas dos funciones integrables \(f,g:[a,b]\to R\), el área de la superficie limitada por la gráfica de \(f\), la gráfica de \(g\) y las rectas \(x=a,x=b\) viene dada por

\[ A=\int_a^b |f(x)-g(x)| dx \]

Para poder calcular esta integral, en la práctica tenemos que aplicar la definición de valor absoluto y la propiedad de aditividad de la integral respecto a subintervalos.

Remark

Fíjate que, como caso particular, si queremos calcular la superficie limitada entre una función \(f\) (positiva o no) y el eje \(OX\), tendremos que hacer:

\[ A=\int_a^b |f(x)-0| dx = \int_a^b |f(x)| dx. \]

Ejemplo:

Calcular el área de la superficie comprendida entre las gráficas de \(y=x^3\) y \(y=x\).

\[ A=\int_a^b |f(x)-g(x)| dx \stackrel{(*)}{=} \]

Para eliminar el valor absoluto, en primer lugar hemos de localizar los puntos de corte entre ambas gráficas, aplicar la aditividad de la integral para subintervalos y comprobar qué gráfica queda por encima de la otra en cada subintervalo:

\[ \stackrel{(*)}{=} \int_{-1}^0 f(x)-g(x) dx+\int_0^1 g(x)-f(x) dx=\int_{-1}^0 (x^3-x) dx+\int_0^1 (x-x^3) dx =\dfrac{1}{2}. \]

También la podemos calcular mediante Sympy:

import sympy as sp
x=sp.symbols('x')
f_exp=x**3
g_exp=x
sp.plot((f_exp,(x,-1,1)),(g_exp,(x,-1,1)))
roots=sp.solve(f_exp-g_exp)
print('Puntos de corte: ',roots)
A=sp.integrate(f_exp-g_exp,(x,-1,0))+sp.integrate(g_exp-f_exp,(x,0,1))
print('El area de la sup comprendida entre las dos graficas es: ',A)
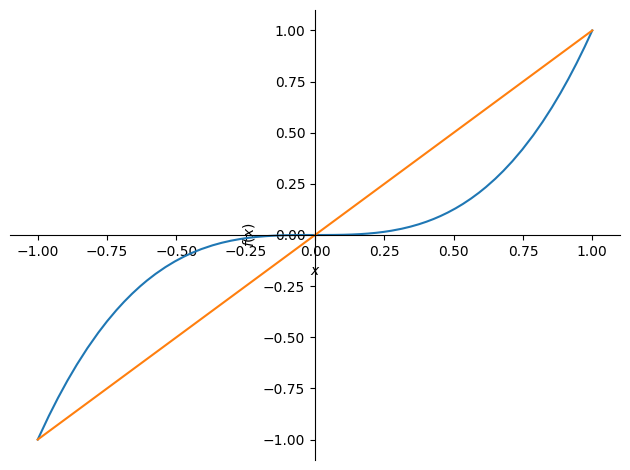
../../_images/00b7f07803004c786d92dbc0ccb0f784988d4561a8592c4bb6c6d474ce5e3e0f.png 
Puntos de corte:  [-1, 0, 1]
El area de la sup comprendida entre las dos graficas es:  1/2

4.6.2. Cálculo de volúmenes#

En esta sección vamos a estudiar cómo aplicar la integral al cálculo de volúmenes de sólidos.

4.6.2.1. Principio de Cavalieri#

Supongamos que tenemos un sólido tridimensional, \(V\), que, al ser cortado por un plano perpendicular al eje \(OX\), para cada \(x\in[a,b]\), produce una sección de área \(A(x)\).

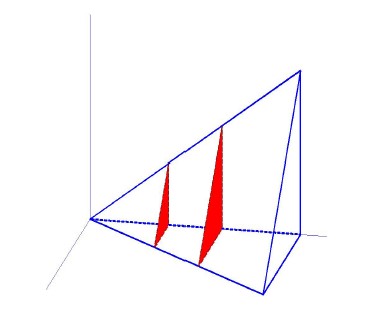
../../_images/cap4_aplicaciones_2.jpg

Entonces el volúmen de \(V\), comprendido entre los planos \(x=a\) y \(x=b\), viene dado por

\[ V=\int_a^b A(x) dx. \]

4.6.2.2. Cuerpos de revolución: método de los discos#

El método de los discos es un caso particular del método de Cavalieri… para figuras de revolución. En este caso, los cortes serán círculos de radio \(|f(x)|\) y, por tanto, con área, \(A(x) = \pi f(x)^2\).

Entonces, dada una función integrable \(f:[a,b]\to R\) el volumen del sólido de revolución generado al rotar alrededor del eje \(OX\) la superficie comprendida entre la gráfica de \(f\), el eje \(OX\), entre \(x=a,x=b\) viene dada por

\[ V=\pi \int_a^b |f(x)|^2 dx. \]

Puedes ilustrar el proceso en la siguiente aplicación de Geogebra, realizada por José Luis Vergara Ibarra: https://www.geogebra.org/m/jxkmyeax

Ejemplo:

Calcular el volumen de una esfera de radio r.

\[ V=\pi \int_{-r}^{r} \left[\sqrt{r^2-x^2}\right]^2 dx=\pi \int_{-r}^{r} r^2-x^2 dx= \pi\left(r^2x-x^3/3\right]_{-r}^{r}=\dfrac{4}{3}\pi r^3 \]
import sympy as sp
x=sp.symbols('x')
r = sp.Symbol('r', positive=True)
f=sp.sqrt(r**2-x**2)
V=sp.pi*sp.integrate(f**2,(x,-r,r))
print('El volumen del sólido de revolución es: ')
display(V)

El volumen del sólido de revolución es:
\[\displaystyle \frac{4 \pi r^{3}}{3}\]

Dadas dos funciones integrables \(f,g:[a,b]\to R\) el volumen del sólido de revolución generado al rotar alrededor del eje \(OX\) la superficie comprendida entre la gráfica de \(f\) y la gráfica de \(g\), entre \(x=a,x=b\) viene dada por

\[ V=\pi \int_a^b |f(x)^2-g(x)^2| dx \]

Ejemplo:

Calcular el volumen del sólido de revolución generado al rotar la superficie comprendida entre las gráficas de \(y=x^3\) y \(y=x\) alrededor del eje X.

\[ V=\pi \int_a^b |f(x)^2-g(x)^2| dx \]

De nuevo, para eliminar el valor absoluto, tenemos que calcular los puntos de corte y emplear la aditividad respecto a intervalos.

\[ =\pi\int_{-1}^1 |f(x)^2-g(x)^2| dx=\pi\int_{-1}^0 g(x)^2-f(x)^2 dx+\pi\int_0^1 g(x)^2-f(x)^2 dx=\pi\int_{-1}^0 (x^2-x^6) dx+\pi\int_0^1 (x^2-x^6) dx =\dfrac{8\pi}{21} \]
import sympy as sp
x=sp.symbols('x')
f=x**3
g=x
roots=sp.solve(f-g)
print('Puntos de corte: ',roots)
V=sp.pi*sp.integrate(g**2-f**2,(x,-1,0))+sp.pi*sp.integrate(g**2-f**2,(x,0,1))
print('El volumen es: ',V)

Puntos de corte:  [-1, 0, 1]
El volumen es:  8*pi/21

También se puede emplear el método de discos para calcular volúmenes de sólidos de revolución generados al rotar una superficie entorno al eje \(OY\). En este caso, obtenemos la misma fórmula, pero la integral ahora es en la variable \(y\), y por tanto la función debe ir escrita también en la variable \(y\)

\[ V=\pi \int_c^d |f(y)|^2 dy \]

Ejemplo:

Calcular el volumen del sólido generado al rotar alrededor del eje \(OY\) la región comprendida entre la parábola \(y=x^2\) entre \(y=0\) y \(y=4\)

\[ V=\pi \int_0^4 [\sqrt{y}]^2 dy=\pi\left( \dfrac{y^2}{2} \right]_{0}^{4}=8\pi \]
import sympy as sp
x,y=sp.symbols('x,y')
sp.plot((x**2,(x,0,2)),(4,(x,0,2)))
f=sp.sqrt(y)
V=sp.pi*sp.integrate(f**2,(y,0,4))
print('El volumen del solido de revolucion es: ',V)
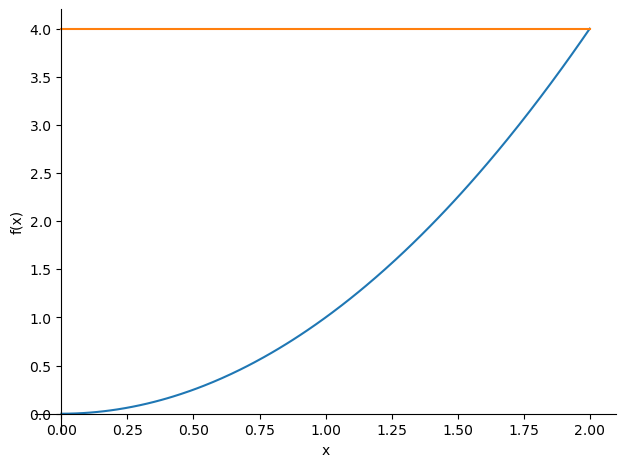
../../_images/2d9ede0c0153d6c0ff1ba65bcf98537eefc44534918b35f7c3f8ffacbb179832.png 
El volumen del solido de revolucion es:  8*pi

Ejercicio:

Calcular el volumen del sólido generado al rotar alrededor del eje \(OY\) la región comprendida entre la parábola \(y^2=8x\) y la recta \(x=2\)

4.6.3. Para seguir practicando#

Puedes encontrar más ejercicios aquí:

Contents